Theorem

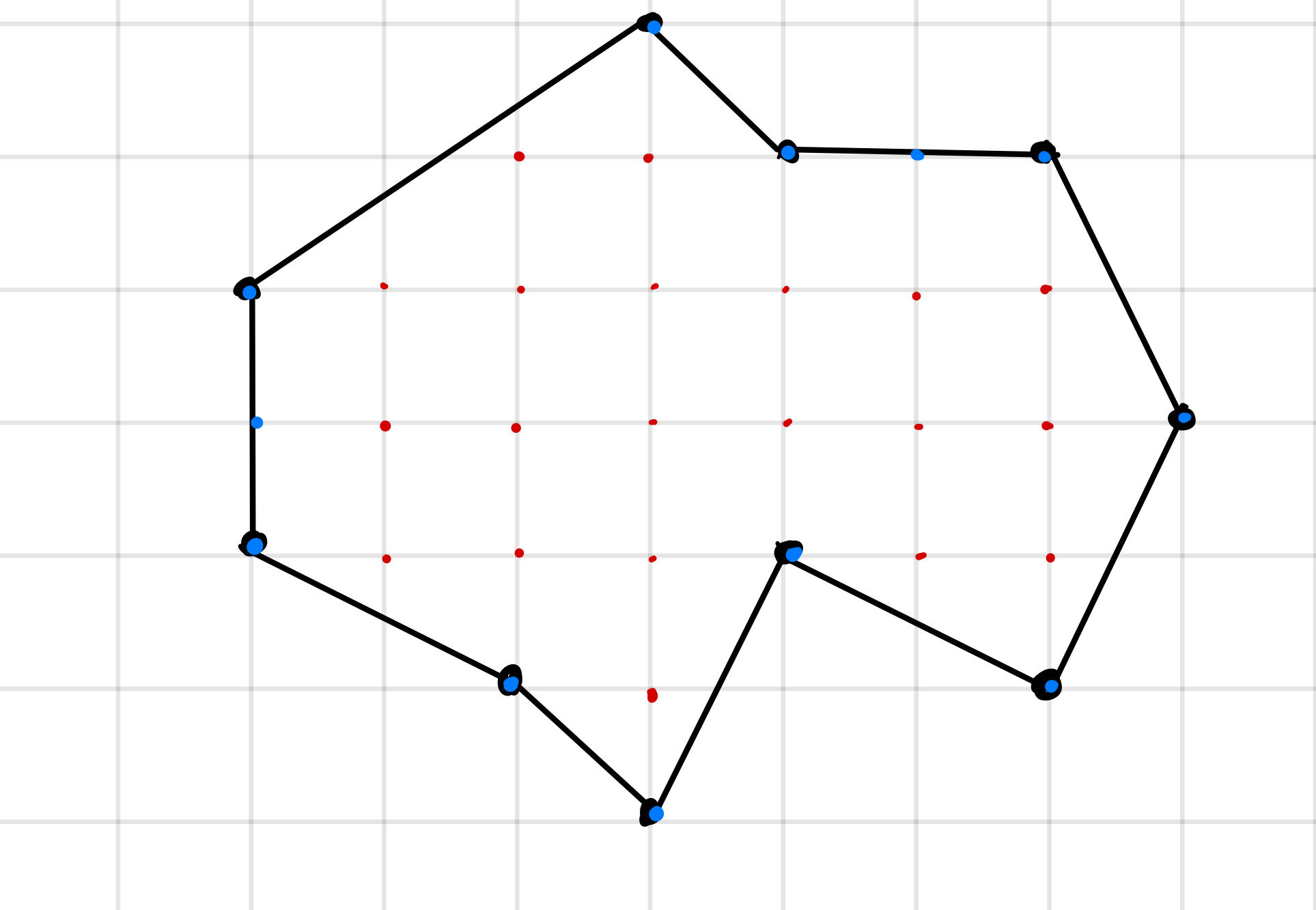
The area of a closed polygon with integer vertices is determined by this formula

Where $B$ is the number of vertices on the boundary (blue in the figure) and $I$ is the number of vertices in the interior of the shape (red in the figure).

Proof

We will use induction on the area of the polygons.

Base Case

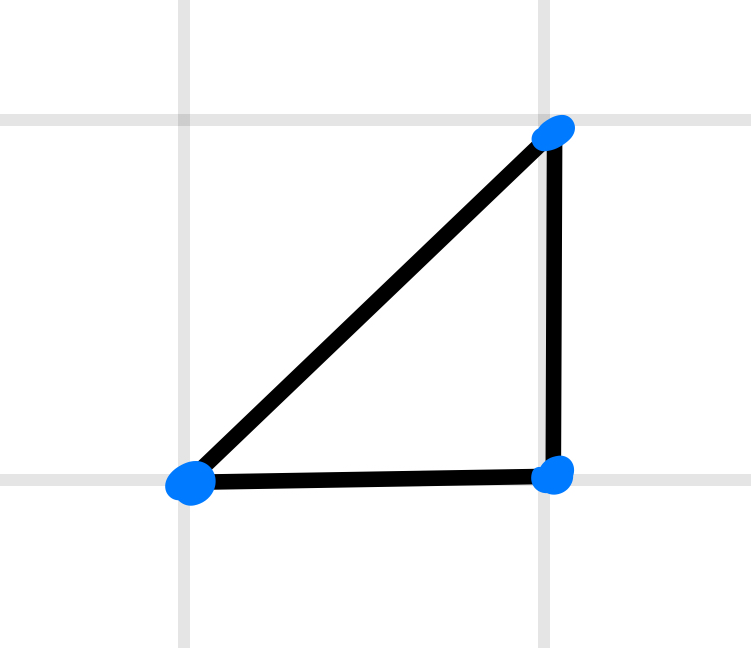
The base case is simply triangles that don't have any vertices on the interior.

It is easy to see that a isoceles right triangle with side length $1$, has area $\frac{1}{2}$. This is clear from the formula for the area of the triangle ($\frac{1}{2}bh$).

A shear takes the form:

So, shears preserve area, and thus, when a triangle is scaled by a shear, it's the area remains the same, so all triangles that are just sheared versions of each other have area $\frac{1}{2}$.

Inductive Step