Overview

I took computer vision many years ago, and I wanted to refresh my knowledge of camera matrices and rendering. So I created this website that displays an infinite stream of confetti. It calculates the movement of confetti in real-time. The code can be found here.

Design

I wanted physics and camera matrices to be the focus of the project, so the UI is spartan.

To describe what is happening, we will assume that in the world, $x,y,z$ are arranged as if we're looking at an $x$-$y$ graph, and $z$ is coming toward us:

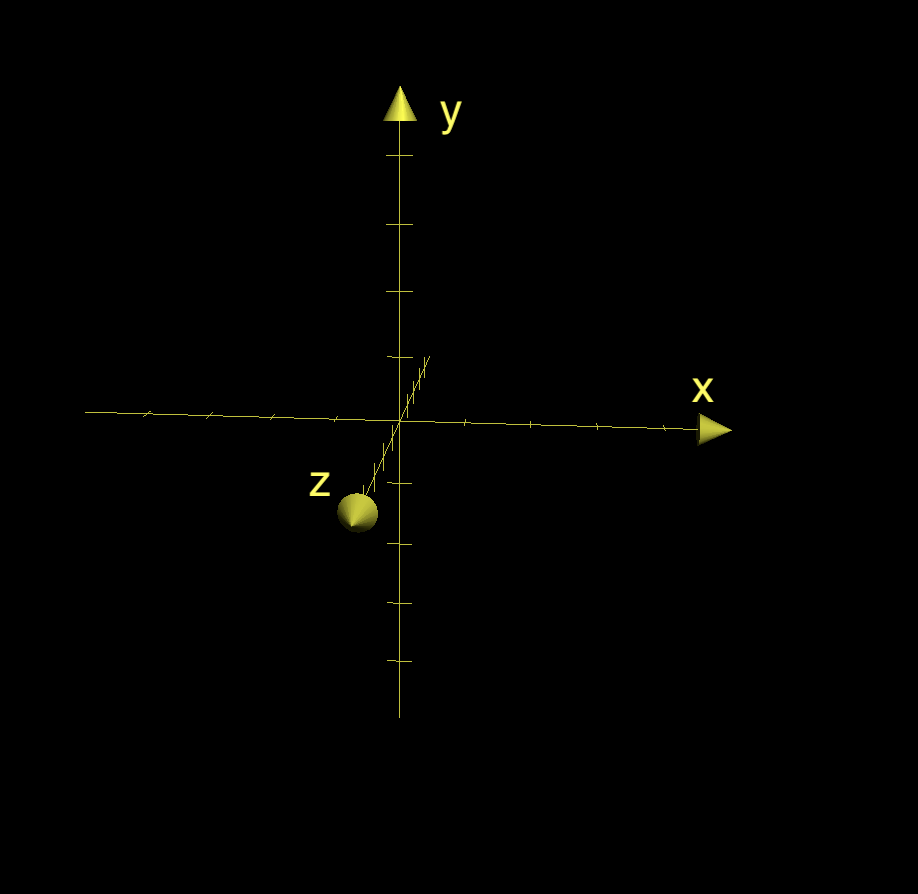
We need to convert a point in that, to a point on the screen, which has coordinates $(0,0)$ in the top left, and increasing $x$ and $y$ going down and right. We can do that using Rt, which is the extrinsic matrix:

This matrix describes how the camera is positioned in relation to the origin. Our rotation is the identity, and our translation is $10$ in the $z$ direction (since our camera is oriented normally at $(0,0,-10)$). Thus, $t_x=t_y=0,t_z=10$. Left multiplying this matrix with a vector will move it 10 units in the $z$ direction (bringing the camera to the origin).

The second matrix we need is the intrinsic matrix:

$f_x, f_y$ are the focal length in pixels of the camera. $u,v$ are the principle point offset (shift in the sensor inside the camera). $s$ is skew. For us, $f_x=f_y=\max(w, h)/2$, which is the maximum of the width and height of the screen. Our skew is 1, and our principle point offsets are 0.

The index.js file holds most of the code, and math.js has some utility functions (like matrix multiplication). There is one function I want to highlight in math.js, and that is world2image. It converts world coordinates to image coordinates. It multiplies $K \cdot [R\mid t] \cdot c$, where $c$ is the world coordinates and rescales the $x,y$ values by $z$. The KRt matrix is a precomputed multiplication of the intrinsic and extrinsic matrices and will take a point in 3D world coordinates and convert it to an $x,y$ coordinate system which is what the camera sees. Finally, we convert the $x,y$ coordinates to screen coordinates.

With the camera matrix calculation out of the way, let's dig into the implementation. I keep track of confetti using its center (in world coordinates), velocity, acceleration, and its two rotation parameters $\theta$ and $\phi$. I used a constant acceleration down at $-9.81$ (for obvious reasons). I initialize the position to be the center of the screen (the origin). I initialize the velocity randomly and uniformly from the top quadrant of a circle. I initialize the rotation parameters, and their deltas randomly.

The main approach is to keep a big array of confetti, and on each rendering step:

• replace confetti that falls off-screen

• update the world coordinates of each confetti (using acceleration, velocity, deltas for rotations, etc.)

• extract the corners of each confetti given their orientation

• use world2image to get the image coordinates of those corners

• draw the quadrilaterals from those image coordinates.

Since we are calculating how each confetti would fall in real-time, large amounts of confetti (or badly optimized browsers), can really slow down a machine. Something to keep in mind if you use the website. Overall, I really enjoyed this project.